M³ – Monologues, MRI, Miscellanea

Looking for reference values of water diffusion?

This is a short advertisement for my web document “Diffusion Coefficients of Water”. If you have ever looked for reference values of the self-diffusion coefficient of water at different temperatures, then chances are that you might like to bookmark the link above.

(If you have never heard of molecular (self-)diffusion, then it’s probably not so relevant for you. As an ultra-short explanation: Self-diffusion is a term for the thermal motion of molecules. If we could look at the individual molecules of a liquid such as water (say, with a really big microscope), then we would see all molecules in constant random motion. This molecular motion is known as the cause of the Brownian motion, which has been observed already in 1827 by the botanist Robert Brown. The extent of this motion is directly related to the temperature of the liquid or – which is essentially the same – to the thermal kinetic energy of the molecules. This motion can be described by a physical quantity called the (self-)diffusion coefficient D, which has units of m² / s. The meaning of a diffusion coefficient of, e. g., D = 2 × 10^–3 mm² / s is that after a time t = 1 s the space “visited” by an average diffusing molecule (in a certain statistical sense) has a size s (i. e., a radius) of s = √( 6Dt ) = √( 12 × 10^–3 mm² ) ≈ 0.1 mm.)

Why is it good to know the exact relationship between the temperature and the diffusion coefficient of water? Typical applications are:

• Using these data, we can determine temperatures by measuring diffusion coefficients of water, e. g., using diffusion-weighted MRI.
• We can check how well our MRI system is calibrated by measuring the temperature conventionally (i. e., with a thermometer) and compare the MRI-determined diffusion coefficient with a reference value.
• An elegant variant of the previous approach is to use an ice-water phantom (i. e., a sample of liquid water floating in a mixture of ice and water such that the temperature is known to be 0 °C) as suggested in a publication by T. L. Chenevert et al. (2011).

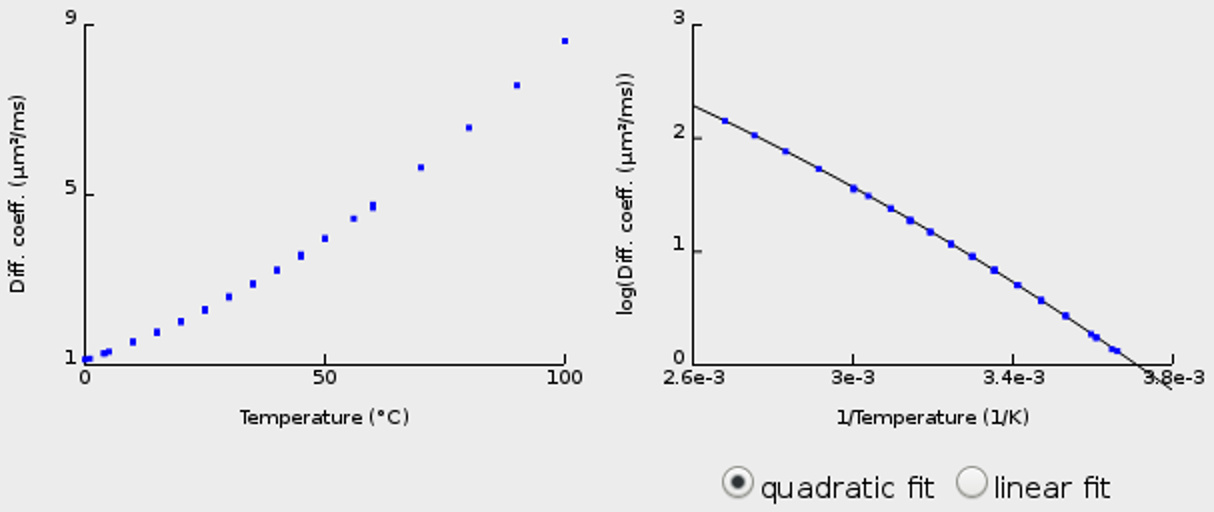
The web document introduced above provides an interactive interface to calculate self-diffusion coefficients of water at different temperatures (or, alternatively, to calculate the temperature corresponding to a given diffusion coefficient). This calculation is based on the results taken from several published articles with exactly this kind of data (namely, measured diffusion coefficients of water at different temperatures).

The web page has actually existed for quite some time (since about 2002), but it was never made public. No (hyper)links to it existed and it was used only by me (and by some colleagues and our Master or PhD students). Thus, I was somewhat surprised when I recently found out that the page is indexed by google and has already been cited in several reports and theses. Consequently, I decided to slightly update its content (and to pretty up its appearance). The most relevant change is that I added a non-linear (quadratic) fit that describes the data in the Arrhenius plot much more accurately (and can be used for data over a greater temperature range) than the previously used linear fit. Note that using the (recommended) quadratic fit, calculated diffusion coefficients for intermediate temperatures around 15 to 30 °C will differ from those of the earlier (linear) version by a few tenths of a percent.